When you ask a Large Language Model (LLM) a question, the model outputs a probability for every possible token in its vocabulary.
After sampling a token from this probability distribution, we can append the selected token to our input prompt so that the LLM can output the probabilities for the next token.
This sampling process can be controlled by parameters such as the famous temperature and top_p.
In this article, I will explain and visualize the sampling strategies that define the output behavior of LLMs. By understanding what these parameters do and setting them according to our use case, we can improve the output generated by LLMs.
For this article, I'll use VLLM as the inference engine and Microsoft's new Phi-3.5-mini-instruct model with AWQ quantization. To run this model locally, I'm using my laptop's NVIDIA GeForce RTX 2060 GPU.
Table Of Contents
· Understanding Sampling With Logprobs ∘ LLM Decoding Theory ∘ Retrieving Logprobs With the OpenAI Python SDK · Greedy Decoding · Temperature · Top-k Sampling · Top-p Sampling · Combining Top-p and Temperature · Min-p Sampling · Conclusion · References
Understanding Sampling With Logprobs
LLM Decoding Theory
LLMs are trained on a finite vocabulary V, which contains all possible tokens x that the model can see and output. A token can be a word, a character, or anything in between.
LLMs take a sequence of tokens x = (x_1, x_2, x_3, ..., x_n) as an input prompt, where each x is an element of V.
Then, the LLM outputs a probability distribution P for the next token, given the input prompt. Mathematically, this can be described as P(x_t | x_1, x_2, x_3, ..., x_t-1).
Which token we choose from this distribution is up to us to decide. Here we can choose between different sampling strategies and sampling parameters.
After selecting the next token, we append the selected token to the input prompt and repeat the cycle.
In the world of LLMs, these probability distributions are often described using logarithmic probabilities, called logprobs.
As shown in the figure below, the logarithmic function is always negative between zero and one.
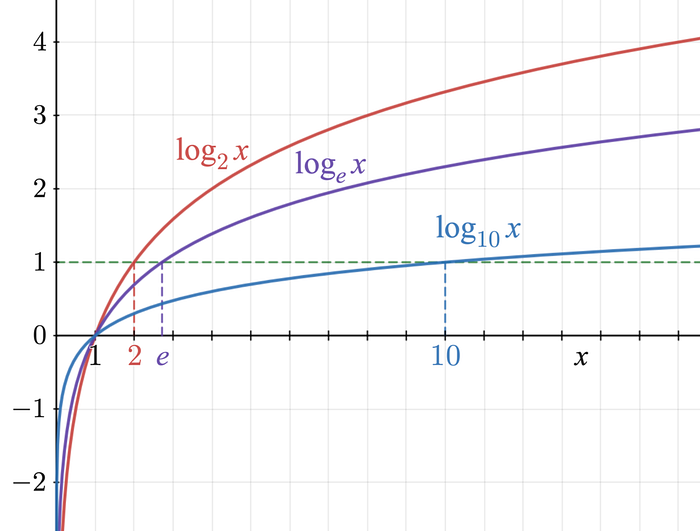
This is why logprobs are negative numbers. A logprob close to zero is a very high probability close to 100%, and a large negative logprob is a probability close to 0%.
Retrieving Logprobs With the OpenAI Python SDK
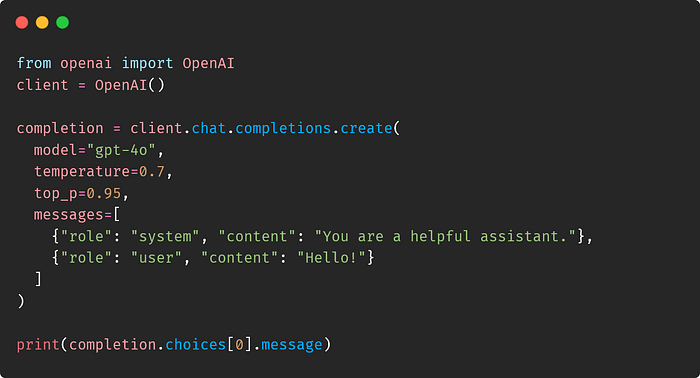
Here is a simple Python script that uses the official OpenAI Python client for chat completion. With these parameters, the model will try to predict the next token given an input prompt.
from openai import OpenAI
client = OpenAI()
completion = client.completions.create(
model="jester6136/Phi-3.5-mini-instruct-awq",
prompt="The quick brown fox jumps over the",
logprobs=10,
temperature=1.0,
top_p=1.0,
max_tokens=1
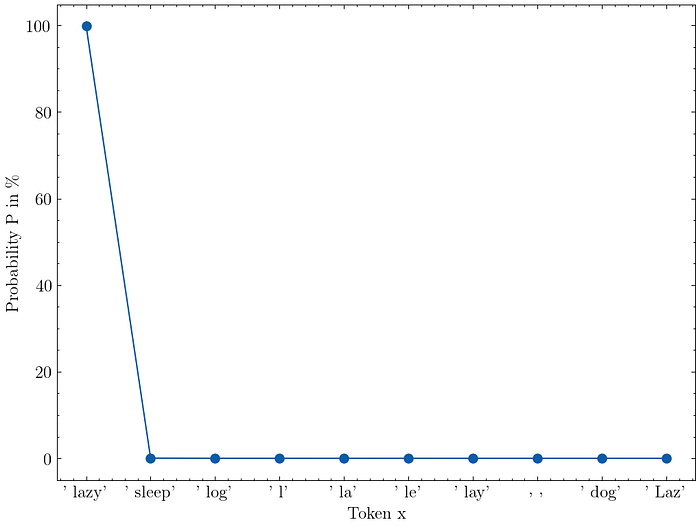
)Below is the token probability distribution for the given sentence. The model chose tokens=[' lazy'] as the next token. We can also see the top 10 logprobs in the list top_logprobs.
logprobs = completion.choices[0].logprobs
print(logsprobs)
>> Logprobs(text_offset=[0],
>> token_logprobs=[-0.0013972291490063071],
>> tokens=[' lazy'],
>> top_logprobs=[{' lazy': -0.0013972291490063071,
>> ' sleep': -7.501397132873535,
>> ' l': -9.095147132873535,
>> ' log': -9.126397132873535,
>> ' la': -9.220147132873535,
>> ' le': -9.313897132873535,
>> ' lay': -9.720147132873535,
>> ' Laz': -9.938897132873535,
>> ' dog': -9.970147132873535,
>> ' ': -9.970147132873535}])We can convert the logprobs to percentages using the following formula:
import numpy as np
probability = 100 * np.exp(logprob)After converting all logprobs, we can see that the token "lazy" has a 99.86% chance of being sampled. This also means that there is a 0.14% chance that something else will be sampled.
Greedy Decoding
The most basic sampling strategy is called greedy decoding. Greedy decoding simply chooses the most likely token each time.
Greedy decoding is a deterministic sampling strategy because there is no randomness involved. Given the same probability distribution, the model will always choose the same next token.
The downside of greedy decoding is that the resulting text is repetitive and not very creative. Imagine writing a text where you always choose the most common words and standard phrases you can think of.
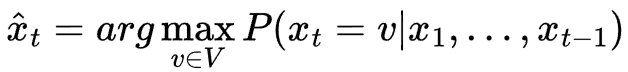
The opposite of deterministic greedy decoding is called stochastic decoding. This is where we start sampling from our distribution to get more creative texts based on chance. Stochastic decoding is what we usually do with LLM outputs.
Temperature
Most people who use LLMs have heard of the temperature parameter.
OpenAI gives the following definition for the temperature parameter:
What sampling temperature to use, between 0 and 2. Higher values like 0.8 will make the output more random, while lower values like 0.2 will make it more focused and deterministic.
After our LLM outputs the probability distribution for the next token, we can modify its shape. The temperature T is a parameter that controls how sharp or flat the probability distribution for the next token becomes.
Mathematically, the new probability distribution P_T after temperature scaling can be calculated as shown in the formula below. z_v is the logprob or logit from the LLM for token v which gets divided by the temperature parameter T.
The temperature scaling formula is essentially a softmax with the additional scaling parameter T.
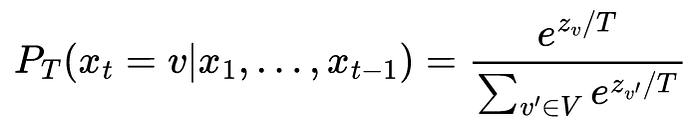
Instead of sampling from the original probability distribution P, we now sample from the new probability distribution P_T.
In the figure below, I have plotted four different probability distributions for the input prompt "1+1=". Obviously, the next token should be 2.
(These are not the full distributions, because I only plotted a few values).
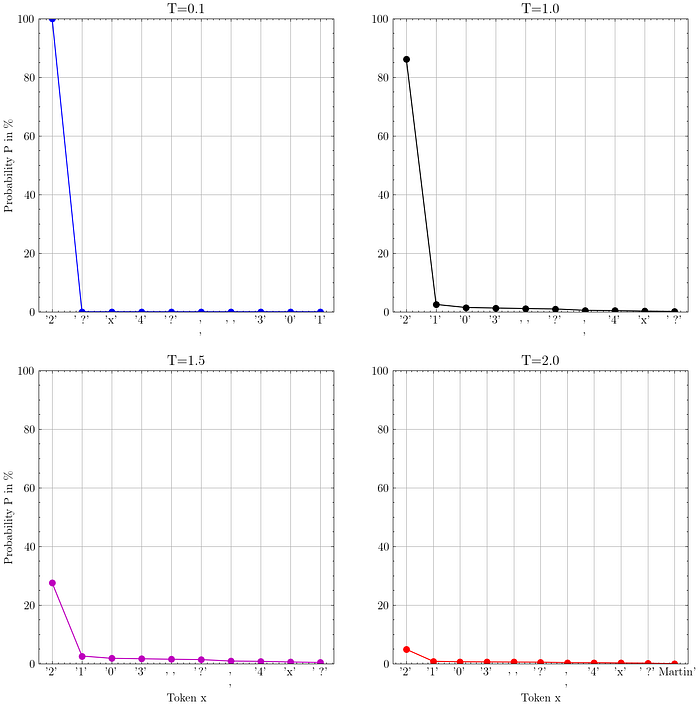
As you can see, the higher the temperature T goes, the flatter the distribution becomes. Where "flat" means that everything becomes more equally likely.
Interestingly, with the default temperature of T=1.0, the obvious answer 2 has a chance of about 85%, which means it is not that unlikely to get a different answer if you sample the output enough times.
With a temperature of T=2.0 the token "2" is still the most likely, but it has a probability of only about 5%. This means that the sampled token is almost completely random at this point. In my opinion, there is no good argument for ever using a temperature of two for this reason.
As stated in the OpenAI documentation, the temperature is a way to make the output more random or more focused. However, since we are only shaping the probability distribution, there is always a non-zero chance of sampling a completely nonsensical token, which can lead to factually incorrect statements or grammatical nonsense.
Top-k Sampling
Top-k sampling simply takes the best k tokens and ignores the rest.
If you set k=1 , you get greedy decoding.
More formally, top-k sampling truncates the probability distribution after the top-k most likely tokens. This means that we set the probability to zero for all tokens in the vocabulary V that are not part of the top-k tokens.
After setting the non-top-k tokens to zero, the remaining distribution is rescaled to sum to one again:
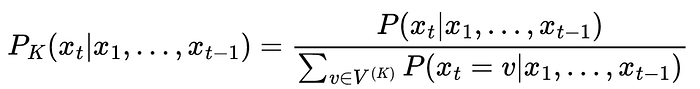
Here is a visualization of top-k sampling with k=4:
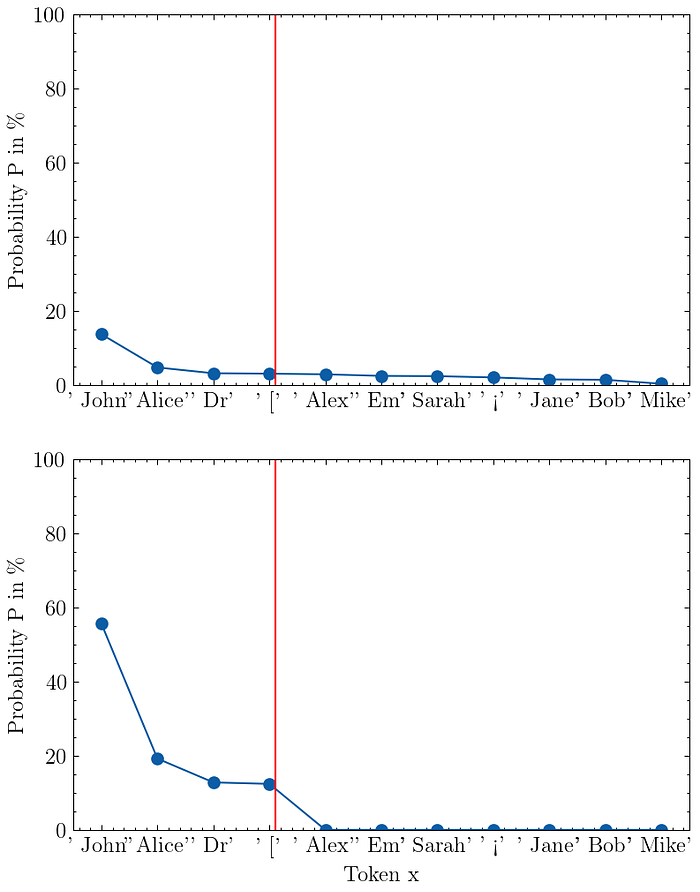
The top figure shows the output distribution of the model. I have drawn a red line to divide the plot into the top-k token on the left side and the rest on the right.
The bottom figure shows the new top-k distribution P_K after truncation and rescaling.
Top-k sampling is not currently a parameter in the OpenAI API, but other APIs, such as Anthropic's, do have a top_k parameter.
One problem with top-k sampling is setting the parameter k. If we have a very sharp distribution, we would like to have a low k to avoid including a lot of highly unlikely tokens in the truncated vocabulary. But if we have a very flat distribution, we would like to have a high k to include a lot of reasonable token possibilities.
Top-p Sampling
Top-p sampling, also called nucleus sampling, is another stochastic decoding method that truncates the probability distribution by removing unlikely tokens from the vocabulary.
OpenAI gives the following definition for the top_p parameter:
An alternative to sampling with temperature, called nucleus sampling, where the model considers the results of the tokens with top_p probability mass. So 0.1 means only the tokens comprising the top 10% probability mass are considered.
In top-p sampling, we define a threshold p for the cumulative probability mass of our tokens. Mathematically, we sum the (sorted) probabilities to their cumulative probability. We include all tokens until the cumulative probability is greater than the threshold p.
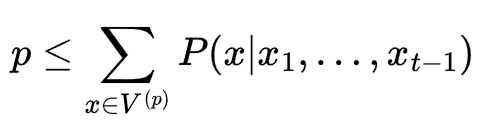
We then rescale the truncated probabilities into a new probability distribution that sums to one.
Here is a visualization for the prompt "I love to" with top-p:
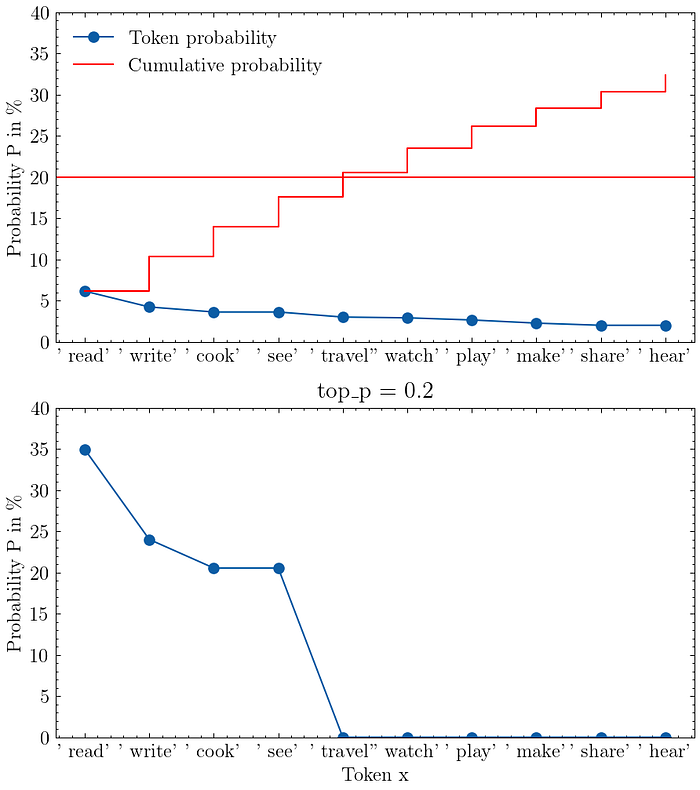
The top figure shows the output distribution of the model, where I have drawn a red line at the 20% threshold, which divides the plot into the top-p token at the bottom and the rest at the top. After rescaling, the bottom figure shows that we are left with only four tokens, the rest have been zeroed out.
I think it always makes sense to remove highly unlikely tokens from the long tail of the logprobs. So, top_p should always be less than 1.0.
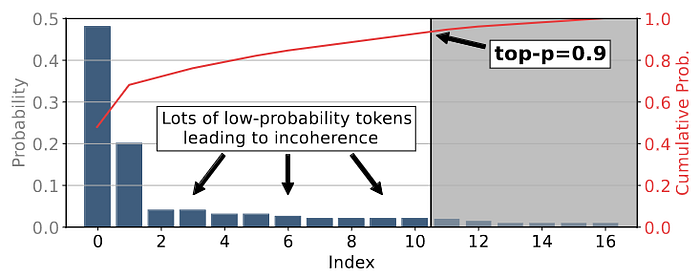
But top-p sampling is not perfect either. The figure below shows a case where top-p sampling includes a lot of low-probability tokens in order to reach the cumulative threshold.
Combining Top-p and Temperature
While I could not find any official documentation from OpenAI, based on community testing, it looks like top_p is used before temperature.
While the OpenAI documentation generally recommends against setting both top_p and temperature, I think there are good reasons to do so.
If you change only the temperature parameter, you flatten or sharpen the probability distribution. This makes the output either more deterministic (low temperature) or more creative (high temperature).
However, the model still samples randomly from the probability distribution. Thus, there is always a chance that the model will sample a highly unlikely token.
For example, the model might sample a character from a foreign language. Or a strange Unicode character. Anything in the model's vocabulary (which is now very large and multilingual) can be sampled.
As a solution, top-p sampling can first eliminate these random tokens, so that a higher temperature can then creatively sample from the remaining reasonable pool of tokens.
Min-p Sampling
There is a relatively new sampling method called min-p sampling from the paper "Min P Sampling: Balancing Creativity and Coherence at High Temperature" [1].
Min-p is also a stochastic decoding method based on truncation that tries to solve the problems of top-p sampling by having a more dynamic threshold p.
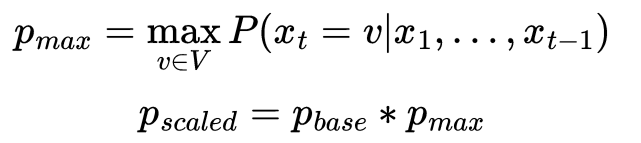
First, we find the maximum probability p_max from the top token in our probability distribution.
This maximum probability is then multiplied by a parameter p_base to give us a minimum threshold p_scaled. We then sample all tokens with a probability greater than or equal to p_scaled. Finally, we rescale the truncated probabilities to a new probability distribution.
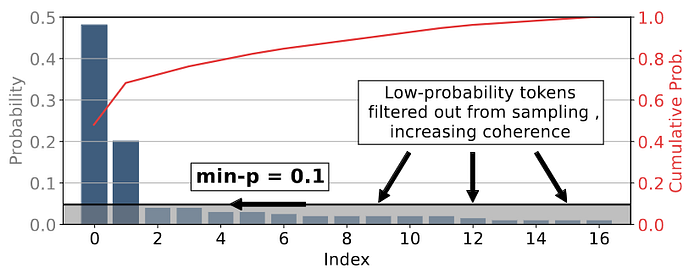
Min-p sampling is already implemented for some backends, such as VLLM and llama.cpp, and I would not be surprised to see it added to the OpenAI API soon.
I have visualized min-p sampling in the figure below with p_base = 0.1 for the input prompt "I love to read a".
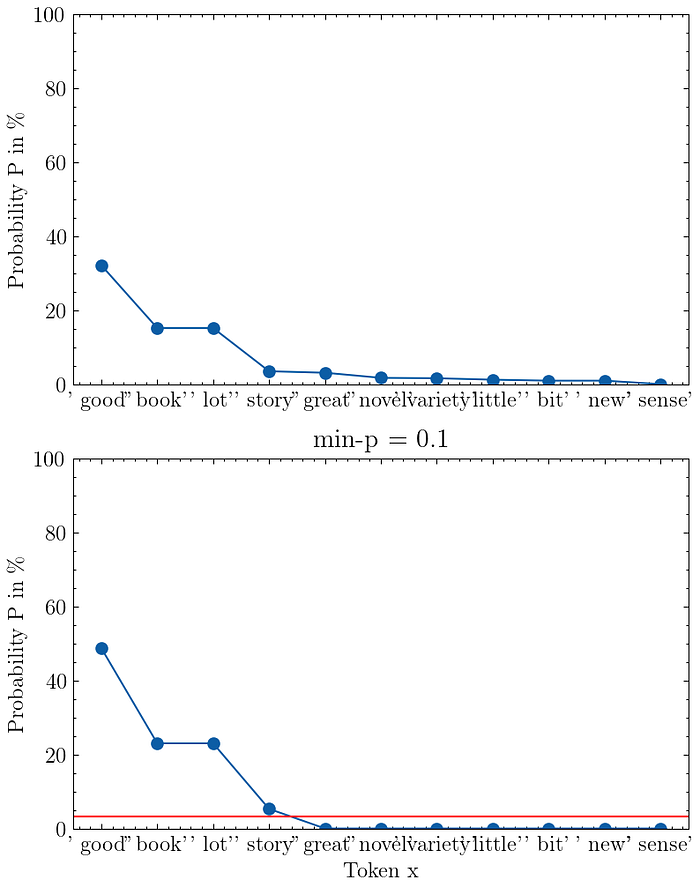
Since the token "good" has a probability of 32% and I set p_base = 0.1 we get a minimum probability threshold of p_scaled = 3.2%, which is the red line in the graph.
Conclusion
Now that we know exactly what the sampling parameters do, we can try to find values that work for our LLM use case.
The most important parameters at this point are temperature and top_p.
The temperature parameter flattens or sharpens the model's output probabilities. However, there is always a chance to sample a completely nonsensical token. In the end, we are still rolling the dice when sampling the next token, given our probability distribution.
The top_k and top_p parameters truncate the probability distribution, i.e., they remove unlikely tokens from the set of possible candidates. However, if we are unlucky, top_k and top_p may remove either too many good candidates or not enough bad candidates.
If your LLM framework supports min-p sampling, you should try it.
References
[1] N. N. Minh, A. Baker, A. Kirsch, C. Neo, Min P Sampling: Balancing Creativity and Coherence at High Temperature (2024), arXiv:2407.01082
[2] A. Holtzman, J. Buys, L. Du, M. Forbes, Y. Choi, The Curious Case of Neural Text Degeneration (2019), Proceedings of International Conference on Learning Representations (ICLR) 2020