Causal Discovery with Mixed Data using pgmpy

Causal discovery with mixed data can be tricky because most methods assume everything is purely discrete or purely continuous. As a result, we often end up dropping variables or turning continuous features into categories — basically throwing away valuable information. However, newer techniques now handle truly mixed datasets, and the Python package pgmpy includes some of these newer methods.

In this post, we'll dive into how pgmpy tackles this problem by walking through an example with the Adult Income dataset from the UCI repository. This dataset features a blend of continuous variables (like Age and HoursPerWeek), ordinal variables (Education levels), and categorical variables (e.g., Workclass, Occupation, and Income).

Setting Up the Dataset

df = pd.read_csv("https://raw.githubusercontent.com/pgmpy/pgmpy/refs/heads/dev/pgmpy/tests/test_estimators/testdata/adult_proc.csv", index_col=0)
df.Education = pd.Categorical(
    df.Education,
    categories=[
        "Preschool",
        "1st-4th",
        "5th-6th",
        "7th-8th",
        "9th",
        "10th",
        "11th",
        "12th",
        "HS-grad",
        "Some-college",
        "Assoc-voc",
        "Assoc-acdm",
        "Bachelors",
        "Prof-school",
        "Masters",
        "Doctorate",
    ],
    ordered=True,
)
df.Workclass = pd.Categorical(df.Workclass, ordered=False)
df.MaritalStatus = pd.Categorical(df.MaritalStatus, ordered=False)
df.Occupation = pd.Categorical(df.Occupation, ordered=False)
df.Relationship = pd.Categorical(df.Relationship, ordered=False)
df.Race = pd.Categorical(df.Race, ordered=False)
df.Sex = pd.Categorical(df.Sex, ordered=False)
df.NativeCountry = pd.Categorical(df.NativeCountry, ordered=False)
df.Income = pd.Categorical(df.Income, ordered=False)

Now we have a mixed dataset with everything neatly labeled: Age and HoursPerWeek are continuous, Education is ordinal, and the rest are categorical. An important point to note here is that this dataset is quite challenging for causal discovery algorithms due to a couple of reasons: 1) It contains mixed variables, 2) The categorical variables are very high-dimensional, for example, NativeCountry has 25 categories, Occupation has 13 categories. Both constraint-based and score-based methods struggle in such high-dimensional scenarios.

Constraint-Based Discovery with the PC Algorithm

The PC algorithm learns the causal structure by systematically performing Conditional Independence (CI) tests over the dataset. The challenge here is that most of these CI tests have been developed for purely discrete or continuous datasets. However, a recent residualization-based CI test [1] for mixed data bridges this gap. pgmpy implements a variant of this method by utilizing the residualizing idea with a measure of association based on canonical correlations. In pgmpy, we can use this CI test in the PC algorithm by specifying ci_test="pillai" argument.

from pgmpy.estimators import PC
estimated_pdag = PC(df).estimate(ci_test='pillai')
estimated_pdag.to_graphviz().draw('adult_pillai.png', prog='dot')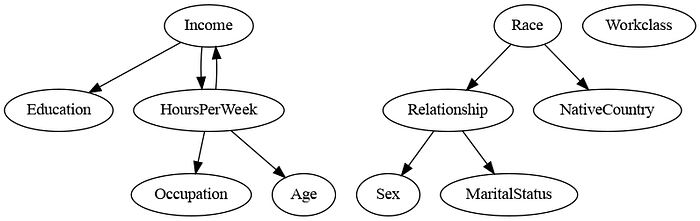

CPDAG learned using PC algorithm

Score-Based Discovery with GES

The score-based methods for causal discovery iteratively make modifications to the model such that the score improves in each iteration. However, similar to CI tests for PC algorithm, most of the scoring methods for these algorithms have been developed for either discrete or continuous variables. pgmpy implements a conditional Gaussian scoring method [2] for tackling mixed variable scenarios. This conditional Gaussian assumption allows us to compute the log-likelihood of the data. We can use the AIC and BIC variants of this log-likelihood by specifying the arguments scoring_method='bic-cg' or scoring_method='aic-cg' . Below is an example using the GES algorithm.

from pgmpy.estimators import GES
estimated_dag = GES(df).estimate(scoring_method='bic-cg')
estimated_dag.to_graphviz().draw('adult_hill.png', prog='dot')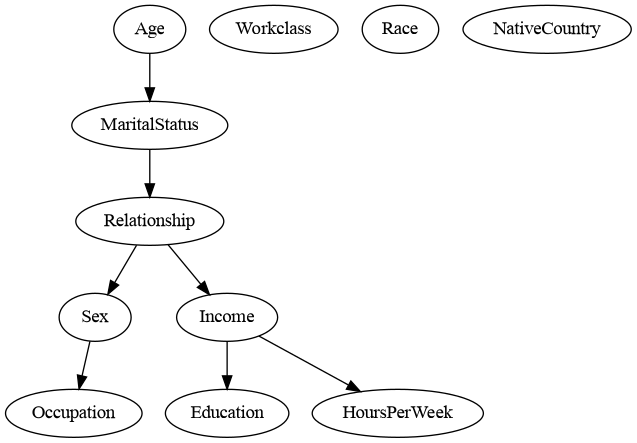

DAG learned using GES algorithm

Wrapping Up

We've just explored how pgmpy handles causal discovery in mixed datasets. The examples, while illustrative, aren't exactly stellar — both the PC and GES models missed edges we'd intuitively expect (like Workclass → Income). That's because the Adult dataset is challenging for causal discovery algorithms becuase of high-dimensional variables like NativeCountry and Occupation . One effective way to boost these algorithms' performance is by injecting domain expertise or "expert knowledge" into the model building process. If you're curious about how that works, check out my other post on using pgmpy while specifying expert knowledge or using an LLM for expert knowledge: https://medium.com/gopenai/llms-for-causal-discovery-745e2cba0b59

References

[1] Ankan, Ankur, and Johannes Textor. "A simple unified approach to testing high-dimensional conditional independences for categorical and ordinal data." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 37. 2023.